数字图像处理期末复习
本文最后更新于:2024年7月4日 凌晨
数字图像基础
图像的获取与感知
图像的获取
图像通常使用感光传感器获取,感光传感器是一种能够将光信号转换为电信号的器件。常见的感光传感器有CCD和CMOS。
| CCD | CMOS | |
|---|---|---|
| 原理 | 电荷耦合器件 | 互补金属氧化物半导体 |
| 耗电量 | 高 | 低 |
| 价格 | 昂贵 | 便宜 |
| 速度 | 慢 | 快 |
| 噪声 | 低 | 高 |
图像的采样与量化
图像的采样是指对一张图片的坐标轴进行数字化,将连续的坐标轴转换为离散的坐标轴。
图像的量化是指对幅度值进行数字化,将连续的幅度值转换为离散的幅度值。
从连续图像的顶部开始,按照一定的间隔,取样点,得到一系列的采样点,这些采样点就是离散图像的像素点。
他的质量取决于一下几个因素:
- 样本数量(空间分辨率)
- 灰度级(灰度采样率)
图像采集系统
图像采集系统其实是一些列图像函数的映射变换步骤,分为一下几个步骤:
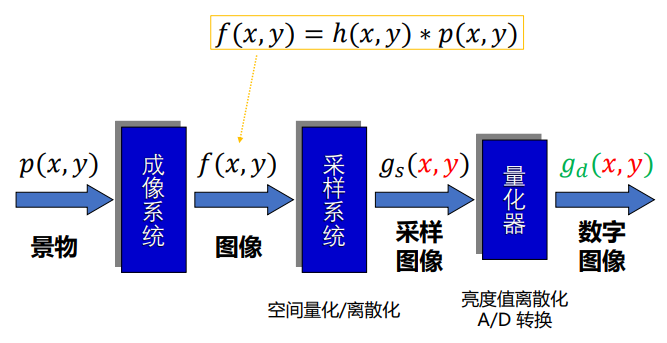
图像的表示
图像的表示有以下几种方式:
- 以(x,y,z)三元组表示
- 以矩阵表示
- 可视的灰度图像
灰度级是指图像中的灰度值的级别,灰度级越高,图像的质量越好。通常为2的指数次幂。
动态范围是指图像中最大灰度值与最小灰度值的比值。
对比度是指图像中最大灰度值与最小灰度值的差值。
空间分辨率是指图像中单位长度内的像素数目。通常用dpi表示。
像素间的关系
邻接关系
- $N_4(p)$邻接:上下左右
- $N_D(p)$邻接:对角线
- $N_8(p)$邻接:上下左右和对角线
V是用于定义邻接/连接关系的像素集合,V的元素称为像素的邻接元素。
- 4邻接:$V = {p_1, p_2, p_3, p_4}$
- 8邻接:$V = {p_1, p_2, p_3, p_4, p_5, p_6, p_7, p_8}$
- m邻接:$V = {p_1, p_2, \cdots, p_m}$ 先四路,四路不行再邻接
通路
从一个像素到另一个像素的路径称为通路。如果路径上的像素都是邻接的,那么这个路径称为邻接通路。
距离
- 曼哈顿距离:$d_4(p_1, p_2) = |x_1 - x_2| + |y_1 - y_2|$
- 欧几里得距离:$d_2(p_1, p_2) = \sqrt{(x_1 - x_2)^2 + (y_1 - y_2)^2}$
- 切比雪夫距离:$d_8(p_1, p_2) = \max(|x_1 - x_2|, |y_1 - y_2|)$
图像的计算
图像的计算是指对图像进行一些数学运算,常见的有:
- 加法
- 减法
- 乘法
- 除法
在计算时候,按照每张图像中的对应像素进行计算,例如
$$
f(x,y) + g(x,y) = h(x,y)
$$
对应的h(x,y)的矩阵中的每个元素都是f(x,y)和g(x,y)对应元素的和。
$$
\begin{bmatrix}
a_11 & a_12 \
a_21 & a_22
\end{bmatrix}
\begin{bmatrix}
b_11 & b_12 \
b_21 & b_22
\end{bmatrix}
=
\begin{bmatrix}
a_11 + b_11 & a_12 + b_12 \
a_21 + b_21 & a_22 + b_22
\end{bmatrix}
$$
例题
例题1
考虑图片所示的图像子集,
- 令 $V = {0,1}$ ,计算p,q之间的4通路,8通路
- 令 $V = {1,2}$ ,重新计算上述过程
$$
\begin{matrix}
&3 & 1 & 2 & 1 & <- q\
&2 & 2 & 0 & 2\
&1 & 2 & 1 & 1\
p->& 1 & 0 & 1 & 2\
\end{matrix}
$$
该图没有4通路,有8通路,通路为:$p \to (1,1) \to (1,2) \to (2,3) \to (3,4) \to (4,4) \ to q$, 8通路下的距离为4,m通路下的距离为5
该图有4通路,有8通路,通路为:$p \to (1,1) \to (1,2) \to (2,3) \to (3,4) \to (4,4) \ to q$, 8通路下的距离为4,m通路下的距离为5
懒得写问题了
图像增强与空间滤波
图像空间的点处理增强
灰度变换
灰度变换是指对图像的每个像素进行灰度值的变换,常见的灰度变换函数有:
- 图像求反 $s = L - 1 - r$
- 对数变换 $s = c \log(1 + r)$
- 幂次变换 $s = c \times r^{\gamma}$
- 分段线性变换 $s = \begin{cases} \frac{s_1}{r_1} r & 0 < r_1 \leq r_2 \ \frac{s_2-s_1}{r_2-r_1}[r-r_1] + s_1 & r_1 < r \leq r_2 \ \frac{L-1-s_2}{L-1-r_2}[r-r_2] + s_2 & r_2 < r \leq L-1 \end{cases}$
- 灰度切割 $s = \begin{cases} 0 & r < r_1 \ r & r_1 \leq r \leq r_2 \ 0 & r > r_2 \end{cases}$ 突出图像中的某个区域
- 位级操作 $s = r \oplus m$ 位级操作是指对图像的每个像素进行位级操作,常见的有与、或、非、异或等操作
直方图处理
- 令 $r_k$ 为图像中灰度值为k的像素数目,$n$为图像的总像素数目,$p_r(k) = \frac{r_k}{n}$为灰度值为k的像素的概率密度函数,$s_k = T(r_k)$为灰度值为k的像素的变换后的灰度值,$p_s(k)$为灰度值为k的像素的概率密度函数,$p_s(k) = \frac{s_k}{n}$
直方图均衡化
直方图均衡化是指将图像的直方图变换为均匀分布的直方图:
灰度变换函数 $s = T(r) = (L-1) \sum_{j=0}^{r} p_r(j)$
步骤
- 计算原始图像的直方图:首先,需要计算图像的直方图,即统计图像中每个像素值的频率。
- 计算累积分布函数(CDF):基于直方图,计算累积分布函数。CDF 是直方图的一个累积版本,表示小于或等于某个像素值的像素占总像素的比例。
- 创建直方图均衡化映射:使用 CDF 来创建一个映射,该映射将原始图像的像素值映射到新的像素值,以此来均衡直方图。这通常通过将 CDF 的值线性映射到整个可用的像素值范围来实现。
- 应用映射到原始图像:将上一步得到的映射应用到原始图像的每个像素上,以生成新的像素值,从而得到直方图均衡化后的图像。
直方图规定化
直方图规定化是指将图像的直方图变换为指定的直方图:
步骤
- 计算原始图像的直方图,进行均衡化
- 计算目标图像的直方图,进行均衡化
- 将目标图像的均衡化直方图映射到原始图像的均衡化直方图上
- 整理映射函数,计算最后的直方图概率
空间滤波
空间滤波是指对图像的每个像素进行滤波操作。
滤波器由aka末班、窗口、核组层
- 核是一个矩阵,用于对图像进行滤波操作,大小定义了运算的领域,系数定义了滤波的方式
- 窗口是核在图像上滑动的区域
- 通常情况下,核的大小是奇数,窗口的大小是核的大小
空间滤波就是在待处理的图像中,逐点移动模板。对每个像素点的像素值,通过与其邻域像素值的加权和来进行处理,以达到图像平滑、锐化、边缘检测等目的。
常见的滤波器有:
平滑滤波器
- 线性平滑滤波器,核的矩阵为 $\frac{1}{9} \begin{bmatrix} 1 & 1 & 1 \ 1 & 1 & 1 \ 1 & 1 & 1 \end{bmatrix}$
- 非线性中值滤波器,
锐化滤波器
- 梯度算子法,Sobel算子,核的矩阵为 $\begin{bmatrix} -1 & 0 & 1 \ -2 & 0 & 2 \ -1 & 0 & 1 \end{bmatrix}$,Preiwitt算子,核的矩阵为 $\begin{bmatrix} -1 & 0 & 1 \ -1 & 0 & 1 \ -1 & 0 & 1 \end{bmatrix}$
- 拉普拉斯滤波器,核的矩阵为 $\begin{bmatrix} 0 & -1 & 0 \ -1 & 4 & -1 \ 0 & -1 & 0 \end{bmatrix}$
低通滤波器
低通滤波器主要用于处理图像边缘和噪声,常见的有:
- 理想低通滤波器:物理上无法实现,会出现振铃现象,图像会出现严重模糊
- 巴特沃斯低通滤波器:核的矩阵为 $\frac{1}{1 + (\frac{D(u,v)}{D_0})^{2n}}$,$D(u,v)$为频率域中的距离,$D_0$为截止频率,$n$为滤波器的阶数
高通滤波器
高通滤波器主要用于增强图像的边缘和细节
- 理想高通滤波器:物理上无法实现,会出现振铃现象,图像会出现严重模糊
- 巴特沃斯高通滤波器:核的矩阵为 $1 - \frac{1}{1 + (\frac{D(u,v)}{D_0})^{2n}}$,$D(u,v)$为频率域中的距离,$D_0$为截止频率,$n$为滤波器的阶数
图像变换与频域滤波
一维傅里叶变换
傅里叶变换是一种信号处理技术,用于将信号从时域转换到频域。傅里叶变换的基本思想是,任何一个周期信号都可以看作是一系列正弦波的叠加。
傅里叶变换基础
连续信号的傅里叶变换公式为:
$$
F(\omega) = \int_{-\infty}^{\infty} f(t) e^{-j\omega t} dt
$$
其中,$F(\omega)$为频率域中的信号,$f(t)$为时域中的信号,$\omega$为频率
离散信号的傅里叶变换公式为:
$$
F(k) = \sum_{n=0}^{N-1} f(n) e^{-j\frac{2\pi}{N}kn}
$$
其中,$F(k)$为频率域中的信号,$f(n)$为时域中的信号,$k$为频率
傅里叶变换性质
彩色图像处理
彩色图像的表示
彩色图像的表示有以下几种方式:
- RGB模型:RGB模型是将颜色分为红、绿、蓝三个通道,通过调节三个通道的亮度来调节颜色
- CMYK模型:CMYK模型是将颜色分为青、品红、黄、黑四个通道,通过调节四个通道的亮度来调节颜色
- HSI模型:HSI模型是将颜色分为色调、饱和度、强度三个通道,通过调节三个通道的亮度来调节颜色
彩色图像的增强
彩色图像的增强有以下几种方式:
- 直方图均衡化
- 直方图规定化
- 空间滤波
伪彩色图像
伪彩色图像是指将灰度图像转换为彩色图像,通过灰度在RGB频道上的映射,将灰度图像转换为彩色图像。